
Finding the Angle of the Illusion
When we do the gallery wrap on our canvas prints, I usually take just a tad along the edge of the image and digitally stretch it to several times its original width to wrap around the edge of the frame. The main reason we do this, besides aesthetics, is so less of the margin is lost around the edge, which could be a blessing if it prevents an important part of your subject from disappearing around the corner because you zoomed or cropped in too tight. When we do that stretching, we set up an optical illusion. As you move to the side of the image, there will be some angle at which the stretched edge image will appear to be just a continuation of the image on the face of the frame. That angle will depend on how much you stretch it. When discussing this previously, I've left the calculation of that angle as as a exercise for the listener. Now I'll show you how to complete that exercise. If you haven't finished your homework yet, turn away now. Caution: this solution does involve basic trigonometry.

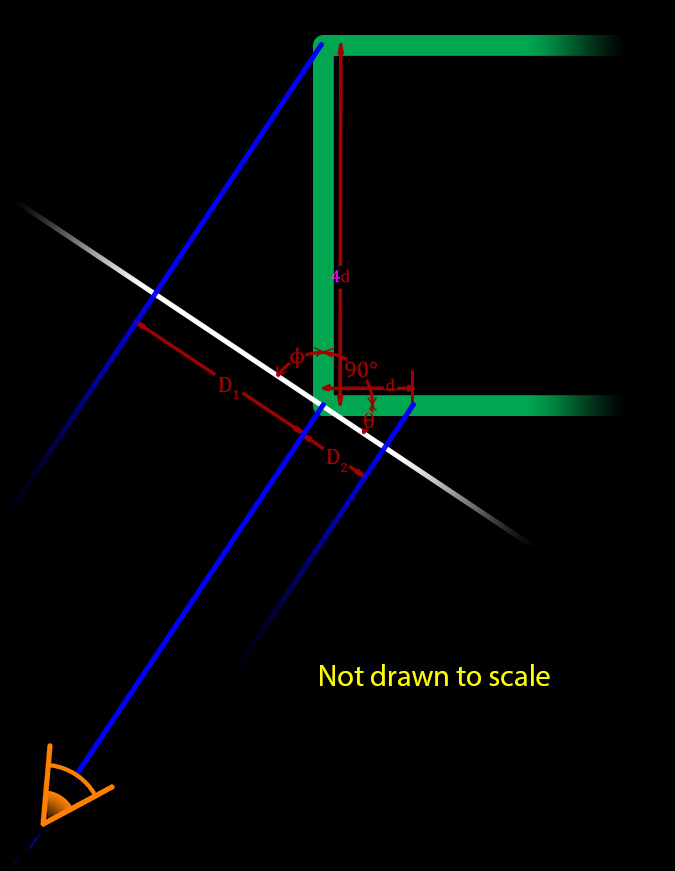
This analysis assumes that you are viewing this image from far enough away that the parallax, or difference in the angle of the light rays (shown in blue) from the various parts of the image to your eye is insignificant (meaning all of the blue lines look almost parallel). The white line in the picture represents a plane parallel to your eye's retina or perpendicular to the blue light rays coming from the image. It is actually just an imaginary construction line conveniently placed so that we can compare the apparent distances (as you see them) of two points that would have been equally distant from the corner of the image had we not stretched one side. This construction line is also placed against the corner of the image so that we can measure the appropriate angles. The green lines represent the canvas that we are viewing. In this exercise we are trying to find the angle Θ so that the distance D1 on the left side (which is how the distance 4d appears to your eye) will look the same as distance D2 on the right (representing your perspective of the distance d on the face of the frame). We are using 4d in this case because that's how much I usually stretch that section. As you can see at the bottom of the green equations, the answer is around 14°. Later we will explore how the angle of illusion Θ changes as we stretch the margins different amounts.
| equations | comments |
| D2/d = cos(Θ) | small triangle relationships |
| Φ = 180°-90°-Θ = 90°-Θ | angle relationships |
| D1/4d = cos(Φ) = cos(90°-Θ) = sin(Θ) | large triangle relationships |
| D ≝ (D1 = D2) | defined only at the illusion angle |
| sin2(Θ)+cos2(Θ) = 1 | Pythagorean Identity |
| D2/16d2+D2/d2 = 1 | substitution |
| (D2+16D2)/16d2 = 1 | algebraic manipulation to isolate D |
| (16+1)D2 = 16d2 | " " |
| D = d*sqrt(16/(16+1)) | " " |
| d*sqrt(16/(16+1)))/d = cos(Θ) | substitute for D in the 1st equation |
| Θ = cos-1(sqrt(16/(16+1))) ≅ 14° | solve for Θ |
To find the angle for different amounts of stretch, all you have to do is change the 4 in the equations with the new stretch ratio, and the 16 with the square of that ratio. For example, if you want to stretch that margin only 3 times (giving a 3:1 ratio), you would replace all 4s with 3s and all 16s with 9s (3 x 3). In the below table I've done that and calculated the answer for the nice round ratios. The ratio of 1:1 represents the case of no stretching, just wrapping. That answer should not be a surprise.

| Stretch Ratio | Illusion Angle |
|---|---|
| 4:1 | 14° |
| 3:1 | 18° |
| 2:1 | 27° |
| 1:1 | 45° |
Note:To see this analysis for a beveled frame, see Finding the Angle of Illusion For Beveled Frames.
If you have any questions about any of this, you can contact us. Hit the Comment Button below if you have any suggestions for improvement.